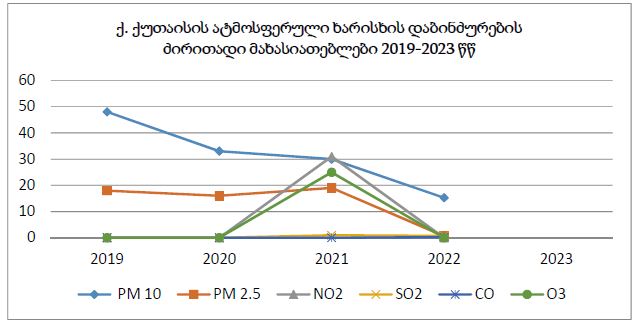
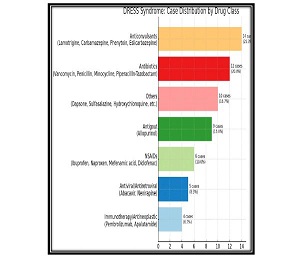
On the conditional distribution of the sum of m − dependent vectors
Downloads
When solving many practical problems, the question arises of constructing statistical estimates of parameters by dependent observations. For example, in a study conducted to determine the rating model of vocational colleges, the data obtained from a survey of students are dependent on each other, due to the fact that they are obtained from the same social group. (R. Chartolani, N. Durglishvili, Z. Kvatadze. Optimization of a State Financing Model of Vocational Colleges. Proc. A. Razmadze Math. Inst. 2015. 169.(2-15), pp. 23-31). Also, the dependence of data in various studies of the geophysical direction cannot be neglected. For example, in the pre-earthquake (preparatory) period, tectonic processes in rocks develop continuously in time, and therefore records of any characteristic taken at discrete points in time depend on each other as manifestations of one whole. Proceeding from similar considerations, when determining the law of distribution of various populations, density estimates are constructed by dependent observations. For example, nonparametric density estimates and estimates of regression coefficients are known, built by observations connected in a Markov chain (Yakowitz Sidney (1989) Nonparametric density and regression estimation for Markov sequences without mixing assumptions. 85721–Journal of Multivariate Analysis, 30: 124-136. Arisona, USA). Conditionally independent observations and observations with a chain dependence are also considered. The accuracies of density estimates constructed by such observations by the metric (Z, Kvatadze, B. Phardjiani. On the Exsactness of Distribution Density Estimates Constructed by Some Class of Dependent Observations. Mathematics and Statistics. 2019 Vol. 7(4), pp. 135-145. SAN JOSE) and by the metric (B. Parjiani, L. Labadze, T. Kvatadze; Georgian Scientists, “On the accuracyby the metric L1 of the density estimation constructed by dependent observations” Vol. 5. Issue 1, pp. 308-321, 2023) are known. To construct statistical estimates based on dependent observations and determine their unbiasedness, it is necessary to know the asymptotic distribution of sums of dependent random variables. At the present stage, the rich theory of summation of independent random variables (Normal Approximation Some Recent Advances. Sazonov V.V. Lecture Notes in Math. V. 79, Berlin, ete.,: Springer. 1981.) is transferred to dependent random variables. In many problems, Markov dependence is used, which is one of the types of weak dependence. Questions of the limiting asymptotic behavior of sums of random variables of various types of dependency (weakly dependent, conditionally independent, connected in a Markov chain) are discussed in many papers. Sums of such random variables are often considered, the joint distribution of which is determined by some control sequence of random elements. Conditionally independent sequences (Bokuchava I. V. Limit theorems for conditionally independent sequences. (in Russian) Teor. Verojatnost. i Primenen. XXIX. (1984). №1, p. 192-193) and sequences with chain dependence are considered. For example, articles by O'Brien (O’ Braien G.L. Limit Theorems for Sum of Chain Dependent Proccesses. U. Appl. Probab., 1974, 11, 582-587), Y. Aleshkevichus (G. YU. Aleshkyavichus, On the central limit theorem for sums of random variables given on a Markov chain. (Russian) Lithuanian Mathematical Collected Works, Vilnius 6 (1966), №. 1, 15−22.), R. Chitashvili, T. Shervashidze, I. Bokuchava, Z. Kvatadze (Bokuchava I., Kvatadze Z., Shervashidze T. On Limit theorem for random vectors controlled by a Marcov chain. Prob. Theory and Math. Stat., Vol. 1, 1986, 239-250. VNU Science Press, Utrecht.) and other authors deal with these issues.In this paper, we discuss the class of sequences of conditionally -independent vectors and the class of sequences of vectors with chain -dependence. (Kvatadze Z., ShervashidzeT. Some limit theorems for I.I.D. and Conditionally independent random variables. The second international Conference, “Problems of Cybernetics and Informatics”. September 10-12, 2008. Baku. Azerbaijan. Section № 4. “Applied Stochastic Analysis”. Institute of Information Technologies of NASA. Printing House of “Information Technology” Baku. 2008. Vol. II, 217-219). In the case of a non-regular ergodic chain, the sequence of functions is defined on a sequence of vectors with a chain -dependence. A representation in matrix form of the limit covariance matrix of the normalized sum of the sequence of these functions is obtained. The fundamental matrix and the corresponding limiting characteristics of the Markov chain in the case of cyclic subclasses are computed using the Cesaro summation. The Levy-Prokhorov metric is often used when considering the convergence of distributions on the space of distribution functions. Therefore, the question of determining the limiting probability of the distribution of the sum of functions falling into a strip consisting of two normal shifted distributions is of natural interest. The article discusses the normalized sum of a sequence of conditionally -dependent vectors. The limiting probability of the conditional distribution of this sum falling into the band consisting of two shifted normal distributions is determined. The covariance matrix of these distributions is expressed by the Markov chain parameters. A similar limiting probability is set for the normalized sum of a sequence of vectors with a chain -dependence.
Downloads
Normal Approximation Some Recent Advances. Sazonov V. V. Lecture Notes in Math. V. 79, Berlin, ete.,:Springer. 1981. https://www.amazon.com/Normal-Approximation-Advances-Lecture-Mathematics/dp/3540108637
Bokuchava I. V. Limit theorems for conditionally independent sequences. (in Russian) Teor. Verojatnost. i Primenen. XXIX. (1984). №1, p. 192-193.
https://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=tvp&paperid=1992&option_lang=rus
Kvatadze Z., Shervashidze T. Some limit theorems for I.I.D. and Conditionally independent random variables. The second international Conference, “Problems of Cybernetics and Informatics”. September 10-12, 2008. Baku. Azerbaijan. Section № 4. “Applied Stochastic Analysis”. www.pci2008.science.az/4/12.pdf. Azerbaijan National Academy of Sciences. Institute of Information Technologies of NASA. Printing House of “Information Technology” Baku. 2008. Vol. II, 217-219.,
https://ict.az/uploads/konfrans/PCI2008/Pci%202008%20v%202/58.pdf
O’ Brien G. L. Limit Theorems for Sum of Chain Dependent Proccesses. U. Appl. Probab., 1974, 11, 582-587. https://www.cambridge.org/core/journals/journal-of-applied-probability/article/abs/limit-theorems-for-sums-of-chaindependent-processes/279300A95BD1750B2E32FFD49AAA1B78
Bokuchava I., Kvatadze Z., Shervashidze T. On Limit theorem for random vectors controlled by a Marcov chain. Prob. Theory and Math. Stat., Vol. 1, 1986, 231-250. VNU Science Press, Utrecht. https://doi.org/10.1515/9783112319000-018 ;
Kvatadze Z., Pharjiani B., Kvatadze TS., One Example of − Dependent Vector’s Sequence. Report of XXXV enlarged session of the seminar of Ilia Vekua Institute of Applied Mathematics (VIAM), of Ivane Javakhisvili Tbilisi State University (TSU). Sept. 16-19., 2021; Volume, 35. pp. 51-54. http://www.viam.science.tsu.ge/enl_ses/vol35/vol35.html ;
Billingsley P. Convergence of probability measures (in Russian). Moscow. “Nauka”, 1971. http://bibliofilspb.ru/item.php?id=15498739 ;
J. G. Kemeny, J. L. Snell, Finite Markov chains. The university series in undergraduate mathematics. USA: Springer-Verlag; 1963, p. 272,
https://www.math.pku.edu.cn/teachers/yaoy/Fall2011/Kemeny-Snell1976.pdf
Kvatadze Z., Kvatadze TS. Limiting Distribution of a Sequence of Functions Defined on a Markov Chain. Proceedings of A. Razmadze Mathematical institute. Vol. 174. 2020. issue 2, 199-205. https://rmi.tsu.ge/transactions/TRMI-volumes/174-2/v174(2)-8.pdf ;
Doob J. Probabilstic processes. (in russian). 1956, M. “Fizmatgiz”. p. 772;
Bežaeva Z. I. Limit theorems for conditional Markov chains (in Russian). Teor. verojatn. i primen., 1971, v. XVI, № 3, p. 437–445.
https://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=tvp&paperid=2257&option_lang=eng;
Kvatadze Z., Shervashidze T., On Limit Theorems for Conditionally Independent Random Variable Controlled by a Finite Markov Chain. Probability Theory and Mathematical Ststistics (Proc. 5th Japan-USSR Symposium on Probability Theory. Kyoto. July 8-14 1986). Lecture Notes in Mathematics. Vol. 1299, p. 250-259 Springer-Verlag, Berlin. etc., 1987. DOI · https://doi.org/10.1007/BFb0078480
Copyright (c) 2023 GEORGIAN SCIENTISTS

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.