ON THE ACCURACY BE THE METRIC OF THE DENSITY ESTIMATION CONSTRUCTED BY DEPENDENT OBSERVATIONS

Abstract

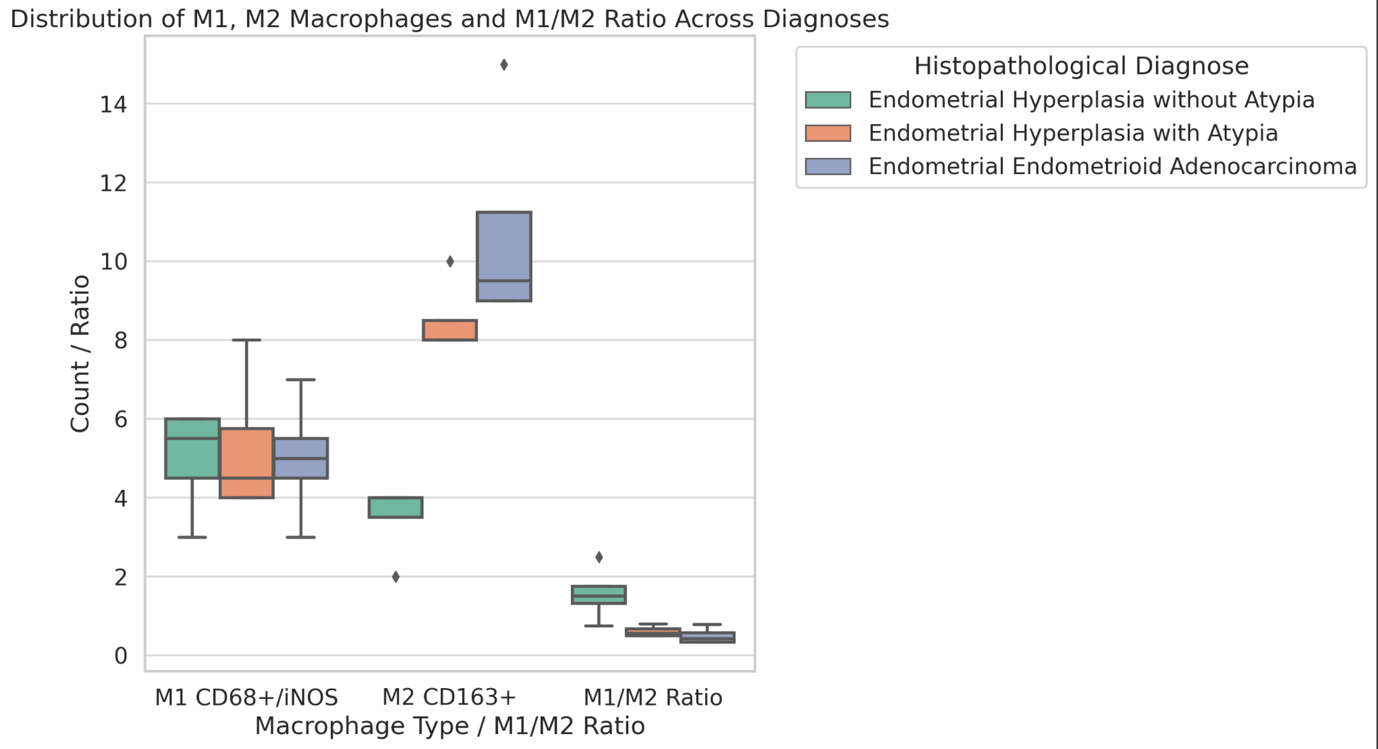
Solving many tasks in modern statistical research (such as studies of financial independence of investment and insurance companies, risk assessment of banking investments, assessment of indicators of financial stability of companies, etc.) requires consideration of dependent observations. Constructing estimates from dependent data is based on a rich historical experience of constructing estimates from independent data. To determine the accuracy of the constructed estimates, it is necessary to study the asymptotics of the sums of dependent random variables. In this process, the research methods of distribution of sums of independent random variables are extended to dependent random variables. Markov dependence is considered. It is one of the forms of weak dependence. Many authors see sums of random variables those joint distributions are determined by some "control" sequence of random elements. By I. Bokuchava, T. Shervashidze and Z. Kvatadze is are determined conditionally independent (Bokuchava I. V. (1984) Limit theorems for conditionally independent sequences. (in Russian) Teor. Verojatnost. i Primenen.-MathNet.Ru XXIX. (1984). №1,. pp. 192-193.1984. Theory of probability and its applications, 1985, 29:1, 190-196; Kvatadze Z., Shervashidze T. (2008) Some limit theorems for I.I.D. and conditionally independent random variables. The Second International Conference, "Problems of Cybernetics and Informatics". September 10-12, 2008. Baku, Azerbaijan. "Applied Stochastic Analysis" www.pci2008.science.az/4/12.pdf. Azerbaijan National Academy of Sciences. INSTITUTE OF INFORMATION TECHNOLOGY. Printing House of "Information Technology" Baku. 2008 . Vol. II. pp. 217-219) and chain dependent (I. V. Bokuchava, Z. Kvatadze, T. Shervashidze, On limit theorems for random vectors controlled by a Markov chain. Probability theory and mathematical statistics, vol. I (Vilnius, 1985), 231-250, VNU Sci. Press, Utrecht, 1987; Kvatadze Z., Sh. ervashidze T. (1987) On limit theorems for conditionally independent random variables controlled by a finite Markov chain. Probability theory and mathematical statistics. (Proc. 5th Japan-USSR Symposium on Probability Theory. Kyoto. 1986). Lecture Notes in Mathematics, 1299: 250-259. Springer-Verlag. Berlin (Germany)) дшьше distributions of normalized sums of random variables.  In the theory of non-parametric estimates, an important place is given to the estimation of the unknown density of the distribution. M. Rosenblatt and E. In the works of Parzen (M. Rosenblatt (1956), Remarks on some nonparametric estimates of a density function. Ann. Math. Statist. 27, Chicago, 832-837, E. Parzen (1962), On estimation of a probability density function and mode . Ann. Math. Statist. 33, Stanford, USA, 1065-1076) a class of robust density estimates constructed from independent observations is considered. The accuracy of these estimates is known (E. (E. A. Nadaraya (1983), Nonparametric estimation of the probability density and regression curve. (in Russian) Tbilisi State Univ. Press, 1983) და  (Devroye L., Györfi L. Nonparametric density estimation: the  view. Wiley series in probability and mathematical statistics, Canada: John Wiley & Sons; 1985. p. 367)  by metrics. The study of the asymptotic behavior of the sums of dependent random variables made it possible to consider dependent observations in the theory of statistical estimates. Nonparametric density estimation and regression coefficient estimations with Markov chain observations are known (Yakowitz Sidney (1989) Nonparametric density and regression estimation for Markov sequences without mixing assumptions. 85721–Journal of Multivariate Analysis, 30: 124-136. Arizona, USA). The accuracy of the density estimation built with dependent observations is also determined by the metric (J. Meloche. Asymptotic behavior of the mean integrated squared error of kernel density estimators for dependent observations. Canadian Journal of Statistics. 2009., 18 (3): p. 205-211). Z. Kvatadze and B. Phardjiani constructed an accurate estimate of the density with conditionally independent and chain-dependent observations and determined their accuracy by a metric in the special case when the governing sequence takes two values ( ) (Z, Kvatadze, B. Phardjiani. On the Exactness of Distribution Density Estimates Constructed by Some Class of Dependent Observations. Mathematics and Statistics. 2019 Vol. 7(4), pp. 135-145. SAN JOSE). The accuracy of the heart estimation constructed by the chain-dependent estimations is also obtained in the metric case as well. In the present work, by Rosenblatt-Parzen-type core estimate of the density is constructed using conditionally independent observations. Are applied obtained by I. Bokuchava, T. Shervashidze and Z. Kvatadze results on the limit distribution of conditionally independent random sums of magnitudes and the accuracy of the constructed estimate are determined by the metric. T. is used during the proof of the theorem. Shervashidze and Z. The method discussed by Kvatadze. On the fixed  trajectory, the sum to be evaluated is expanded into the corresponding sums of the states of the control sequence. These totals are uncorrelated. The components of each sum on the fixed trajectory are independent. The dimensionality of ( ) functions defined on chain states is used (Kvatadze Z., Kvatadze TS. Limiting Distribution of a Sequence of Functions Defined on a Markov Chain. Proceedings of A. Razmadze Mathematical institute. Vol. 174. 2020. issue 2, 199-205) By fixing the trajectory obtained by partitioning the probability space with respect to the induced algebra. The applied method makes it possible to obtain the accuracy of other types of estimates constructed with dependent observations.