სიმკვრივის დამოკიდებული დაკვირვებებით აგებული შეფასების მეტრიკით სიზუსტის შესახებ
ჩამოტვირთვები
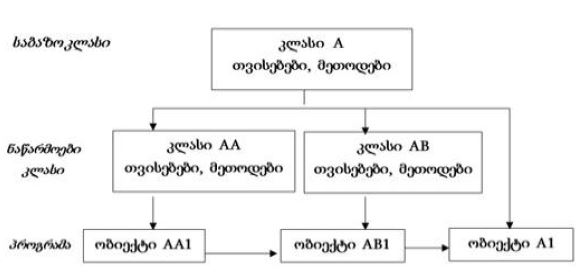
თანამედროვე სტატისტიკურ კვლევებში მრავალი ამოცანის გადაჭრა, (როგორებიცაა მაგალითად საინვესტიციო და სადაზღვევო კომპანიების ფინანსური დამოუკიდებლობის კვლევები, საბანკო ინვესტიციების რისკების შეფასება, კომპანიების ფინანსური სტაბილურობის ინდიკატორების შეფასება და ა. შ.) მოითხოვს დამოკიდებული დაკვირვებების განხილვას. დამოკიდებული მონაცემებით შეფასებების აგება ემყარება დამოუკიდებელი მონაცემებით შეფასებათა აგების მდიდარ ისტორიულ გამოცდილებას. აგებული შეფასებების სიზუსტის დადგენისთვის საჭიროა დამოკიდებული შემთხვევითი სიდიდეების ჯამების ასიმპტოტიკის შესწავლა. ამ პროცესში ხდება დამოუკიდებელ შემთხვევით სიდიდეთა ჯამების განაწილების კვლევის მეთოდების დამოკიდებულ შემთხვევით სიდიდეებზე გავრცობა. განიხილება მარკოვული დამოკიდებულება. ის სუსტად დამოკიდებულების ერთ-ერთი სახეა. მრავალი ავტორი იხილავს ისეთ შემთხვევით სიდიდეთა ჯამებს, რომელთა ერთობლივი განაწილება განისაზღვრება შემთხვევით ელემენტთა რაიმე „მმართველი“ მიმდევრობით. ი. ბოკუჩავამ, თ. შერვაშიძემ და ზ. ქვათაძემ დაადგინეს პირობითად დამოუკიდებელი (Bokuchava I. V. (1984) Limit theorems for conditionally independent sequences. (in Russian) Teor. Verojatnost. i Primenen.-MathNet.Ru XXIX. (1984). №1, pp. 192-193.1984. Theory of probability and its applications, 1985, 29:1, 190-196; Kvatadze Z., Shervashidze T. (2008) Some limit theorems for I.I.D. and conditionally independent random variables. The Second International Conference, “Problems of Cybernetics and Informatics“. September 10-12, 2008. Baku, Azerbaijan. “Applied Stochastic Analysis” www.pci2008.science.az/4/12.pdf. Azerbaijan National Academy of Sciences. INSTITUTE OF INFORMATION TECHNOLOGY. Printing House of “Information Technology” Baku. 2008. Vol. II. pp. 217-219) და ჯაჭვურად დამოკიდებული (I. V. Bokuchava, Z. Kvatadze, T. Shervashidze, On limit theorems for random vectors controlled by a Markov chain. Probability theory and mathematical statistics, vol. I (Vilnius, 1985), 231-250, VNU Sci. Press, Utrecht, 1987; Kvatadze Z., Shervashidze T. (1987) On limit theorems for conditionally independent random variable controlled by a finite Markov chain. Probability theory and mathematical statistics. (Proc. 5th Japan-USSR Symposium on Probability Theory. Kyoto. 1986). Lecture Notes in Mathematics, 1299: 250-259. Springer-Verlag. Berlin (Germany)) შემთხვევითი სიდიდეების ნორმირებული ჯამების ზღვარითი განაწილებები. არაპარამეტრულ შეფასებათა თეორიაში მნიშვნელოვანი ადგილი ეთმობა განაწილების უცნობი სიმკვრივის შეფასებას. მ. როზენბლატის და ე. პარზენის ნაშრომებში (M. Rosenblatt (1956), Remarks on some nonparametric estimates of a density function. Ann. Math. Statist. 27, Chicago, 832-837, E. Parzen (1962), On estimation of a probability density function and mode. Ann. Math. Statist.33, Stanford, USA, 1065-1076) განხილულია დამოუკიდებელი დაკვირვებებით აგებული სიმკვრივის გულოვანი შეფასებების კლასი. ცნობილია ამ შეფასებების სიზუსტე (E. A. Nadaraya (1983), Nonparametric estimation of the probability density and regression curve. (in Russian) Tbilisi State Univ. Press, 1983) და (Devroye L., Györfi L. Nonparametric density estimation: the view. Wiley series in probability and mathematical statistics, Canada: John Wiley & Sons; 1985. p. 367) მეტრიკებით. დამოკიდებულ შემთხვევით სიდიდეთა ჯამების ასიმპტოტური ყოფაქცევის შესწავლამ შესაძლებელი გახადა სტატისტიკურ შეფასებათა თეორიაში დამოკიდებული დაკვირვებების განხილვა. ცნობილია სიმკვრივის არაპარამეტრული შეფასება და რეგრესიის კოეფიციენტების შეფასებები მარკოვის ჯაჭვად შეკრული დაკვირვებებით (Yakowitz Sidney (1989) Nonparametric density and regression estimation for Markov sequences without mixing assumptions. 85721–Journal of Multivariate Analysis, 30: 124-136. Arisona, USA). ასევე დადგენილია დამოკიდებული დაკვირვებებით აგებული სიმკვრივის შეფასების სიზუსტე მეტრიკით (J. Meloche. Asymptotic behavior of the mean integrated squared error of kernel density estimators for dependent observations. Canadian Journal of Statistics. 2009., 18 (3): p. 205-211). ზ. ქვათაძის და ბ. ფარჯიანის მიერ აგებულია სიმკვრივის გულოვანი შეფასება პირობითად დამოუკიდებელი და ჯაჭვურად დამოკიდებული დაკვირვებებით და დადგენილია მათი სიზუსტე მეტრიკით იმ კერძო შემთხვევაში, როდესაც მმართველი მიმდევრობა იღებს ორ მნიშვნელობას ( ) (Z, Kvatadze, B. Phardjiani. On the Exsactness of Distribution Density Estimates Constructed by Some Class of Dependent Observations. Mathematics and Statistics. 2019 Vol. 7(4), pp. 135-145. SAN JOSE). ასევე მიღებულია ჯაჭვურად დამოკიდებული შეფასებებით აგებული გულოვანი შეფასების სიზუსტე მეტრიკით შემთხვევაშიც. წინამდებარე ნაშრომში პირობითად დამოუკიდებელი დაკვირვებებით აგებულია სიმკვრივის როზენბლატ−პარზენის ტიპის გულოვანი შეფასება. გამოყენებულია ი. ბოკუჩავას, თ. შერვაშიძის და ზ. ქვათაძის მიღებული შედეგები პირობითად დამოუკიდებელ შემთხვევით სიდიდეთა ჯამების ზღვარითი განაწილების შესახებ და დადგენილია აგებული შეფასების სიზუსტე მეტრიკით. თეორემის დამტკიცების დროს გამოიყენება თ. შერვაშიძის და ზ. ქვათაძის მიერ განხილული მეთოდი. დაფიქსირებულ ტრაექტორიაზე ხდება შესაფასებელი ჯამის დაშლა მმართველი მიმდევრობის მდგომარეობების შესაბამის ჯამებად. ეს ჯამები არაკორელირებულებია. დაფიქსირებულ ტრაექტორიაზე თითოეული ჯამის შემადგენელი შესაკრებები დამოუკიდებლებია. გამოყენებულია ჯაჭვის მდგომარეობებზე განსაზღვრული () ფუნქციების ზომადობა (Kvatadze Z., Kvatadze TS. Limiting Distribution of a Sequence of Functions Defined on a Markov Chain. Proceedings of A. Razmadze Mathematical institute. Vol. 174. 2020. issue 2, 199-205) ტრაექტორიის დაფიქსირებით მიღებული ალბათური სივრცის დაყოფით ინდუცირებული ალგებრის მიმართ. გამოყენებული მეთოდი შესაძლებლობას იძლევა მიღებულ იქნას დამოკიდებული დაკვირვებებით აგებული სხვა ტიპის შეფასების სიზუსტე.
Downloads
M. Rosenblatt (1956), Remarks on some nonparametric estimates of a density function. Ann. Math. Statist. 27, Chicago, 832-837.
E. Parzen (1962), On estimation of a probability density function and mode. Ann. Math. Statist.33, Stanford, USA, 1065-1076.
G. S. Watson, M.R. Leadbetter (1963) On the estimation of the probability density. Ann. Math. Statist. 34, Toronto, : 480-491.
E. A. Nadaraya (1983), Nonparametric estimation of the probability density and regression curve. (in Russian) Tbilisi State Univ. Press, 1983.
Devroye L., Györfi L. Nonparametric density estimation: the view. Wiley series in probability and mathematical statistics, Canada: John Wiley & Sons; 1985. p. 367.
R. Z. Khasminski, On limiting distributions for sums of conditionally independent random variables. (Russian) Teor. Verojatnosti. i primenen. 6. (1961). №1,.119-125.
G. L. O'Brien, Limit theorems for sums of chain-dependent processes. J. Appl. Probability 11 (1974), 582-587.
Bokuchava I. V. (1984) Limit theorems for conditionally independent sequences. . (in Russian) Teor. Verojatnost. i Primenen.-MathNet.Ru XXIX. (1984). №1,. p. 192-193.1984. Theory of probability and its applications, 1985, 29:1, 190-196
Kvatadze Z., Shervashidze T. (2008) Some limit theorems for I.I.D. and conditionally independent random variables. The Second International Conference, “Problems of Cybernetics and Informatics“. September 10-12, 2008. Baku, Azerbaijan. Section #4. “Applied Stochastic Analysis” www.pci2008.science.az/4/12.pdf. Azerbaijan National Academy of Sciences. INSTITUTE OF INFORMATION TECHNOLOGY. Printing House of “Information Technology” Baku. 2008. Vol. II. pp.217-219.
I. V. Bokuchava, Z. Kvatadze, T. Shervashidze, On limit theorems for random vectors controlled by a Markov chain. Probability theory and mathematical statistics, vol. I (Vilnius, 1985), 231-250, VNU Sci. Press, Utrecht, 1987.
Kvatadze Z., Shervashidze T. (1987) On limit theorems for conditionally independent random variable controlled by a finite Markov chain. Probability theory and mathematical statistics. (Proc. 5th Japan-USSR Symposium on Probability Theory. Kyoto. 1986). Lecture Notes in Mathematics, 1299: 250-259. Springer-Verlag. Berlin (Germany).
Yakowitz Sidney (1989) Nonparametric density and regression estimation for Markov sequences without mixing assumptions. 85721–Journal of Multivariate Analysis, 30: 124-136. Arisona, USA.
J. Meloche. Asymptotic behavior of the mean integrated squared error of kernel density estimators for dependent observations. Canadian Journal of Statistics. 2009., 18 (3): p. 205-211.
Z, Kvatadze, B. Phardjiani. On the Exsactness of Distribution Density Estimates Constructed by Some Class of Dependent Observations. Mathematics and Statistics. 2019 Vol. 7(4), pp. 135-145. SAN JOSE.
Kvatadze Z., Pharjiani B., Construction of a kernel density estimator of Rosenblatt-Parzen type by conditionally independent observations. Proceedings of A. Razmadze Mathematical institute. Vol. 173. 2019. issue 3, 93-102.
Pharjiani B., Kvatadze TS., Kvatadze Z., On an Application of Density Estimation Constructed by Means of Chain Dependent Samples. Report of XXXIV enlarged session of the seminar of I. Vekua Institute of Applied Mathematics (VIAM), of Ivane Javakhisvili Tbilisi State University (TSU). Sept. 16-19. 2020; Volume, 34. pp. 69-72.
Kvatadze Z., Shervashidze T., Some limit theorems for IID and Conditionally independent random variables. The second international Conference, “Problems of Cybernetics and Informatics”. September 10-12, 2008. Baku. Azerbaijan section N 4. “Applied Stochastic Analysis”. Science 14/12.pdf. Azerbaijan National Academy of Sciences. INSTITUTE OF INFORMATION TECHNOLOGY. Printing House of “Information Technology” Baku. 2008. Vol. II, 217-219.
Kvatadze Z., Shervashidze T. On some Limit Theorems for sums and Products of Random Variables. Proceedings of A. Razmadze Mathematical institute. Vol. 150. 2009. 99-104.
Kvatadze Z., Kvatadze TS. Limiting Distribution of a Sequence of Functions Defined on a Markov Chain. Proceedings of A. Razmadze Mathematical institute. Vol. 174. 2020. issue 2, 199-205.

ეს ნამუშევარი ლიცენზირებულია Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 საერთაშორისო ლიცენზიით .